Presentación
Aldair Jose Rincón Baldovino
Fabian Andres Martinez Guerrero
Diego Andres Florez Zabaleta
Yaisir Rico Ortega
lunes, 29 de agosto de 2011
EJERCICIOS
Sistema de 2 ecuaciones con 2 incógnitas
Para la resolución de un sistema de dos ecuaciones con dos incógnitas, de la forma. Dado el sistema de ecuaciones:
Lo representamos en forma de matrices:´Si 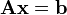 es un sistema de ecuaciones. A es la matriz de coeficientes del sistema,
es un sistema de ecuaciones. A es la matriz de coeficientes del sistema,  es el vector columna de las incógnitas y
es el vector columna de las incógnitas y  es el vector columna de los términos independientes. Entonces la solución al sistema se presenta así:
es el vector columna de los términos independientes. Entonces la solución al sistema se presenta así:
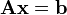 es un sistema de ecuaciones. A es la matriz de coeficientes del sistema,
es un sistema de ecuaciones. A es la matriz de coeficientes del sistema,  es el vector columna de las incógnitas y
es el vector columna de las incógnitas y  es el vector columna de los términos independientes. Entonces la solución al sistema se presenta así:
es el vector columna de los términos independientes. Entonces la solución al sistema se presenta así:Entonces, x e y pueden ser encontradas con la regla de Cramer, con una división de determinantes, de la siguiente manera:Bibliografia
EXPLICACIÓN DEL TEMA
Si pensamos en las columnas del determinante 2x2 (o de la matriz 2x2), como las componentes de un vector del plano x y
|x1 x2|
|y1 y2|
tenemos un vector (x1;y1) y el otro vector es (x2;y2)
***********************
El determinante resuta ser igual al área del paralelogramo cuyos lados son los vectores (x1;y1) (x2;y2) (o el doble del área del triangulo)
**********************
Es que una vez que pensamos a la matriz como un par de vectores el determinante es el la componente perpendicular al plano del producto vectorial de esos vectores
************************
Así el el plano tanto el
área, el producto vectorial y como determinante son conceptos íntimamente relacionados.
*************************
También podes pensar el área del paralelogramo como el producto de la diagonal mayor por la diagonal menor sobre dos.
Vectorialmente la diagonal mayor es la suma de los vectores Digamos (V1+V2)
La diagonal menor es la diferencia entre los vectores
(V1-V2)
Si hacemos el producto vectorial
(V1+V2)^(V1-V2)
Teniendo en cuente que V1^V1=V2^V2=0 (vector cero)
y que V1^V2=-V2^V1
Resulta 2 V1^V2
que dividido dos da V1^V2
Es decir el producto vectorial:
(x1;y1;0)^(x2;y2;0)=
(0;0;x1y2-x2y1)
Por eso un área suele representarse con un vector perpendicular a la superficie.
Si en lugar de dos vectores en el plano (2x2) tengo tres vectores en el espacio (3x3)
el determinante es igual al volumen del paralelepípedo.
(o el doble del tetraedro)
TOMADO DE:http://www.todoexpertos.com/categorias/ciencias-e-ingenieria/matematicas/respuestas/1307147/determinantes
|x1 x2|
|y1 y2|
tenemos un vector (x1;y1) y el otro vector es (x2;y2)
***********************
El determinante resuta ser igual al área del paralelogramo cuyos lados son los vectores (x1;y1) (x2;y2) (o el doble del área del triangulo)
**********************
Es que una vez que pensamos a la matriz como un par de vectores el determinante es el la componente perpendicular al plano del producto vectorial de esos vectores
************************
Así el el plano tanto el
área, el producto vectorial y como determinante son conceptos íntimamente relacionados.
*************************
También podes pensar el área del paralelogramo como el producto de la diagonal mayor por la diagonal menor sobre dos.
Vectorialmente la diagonal mayor es la suma de los vectores Digamos (V1+V2)
La diagonal menor es la diferencia entre los vectores
(V1-V2)
Si hacemos el producto vectorial
(V1+V2)^(V1-V2)
Teniendo en cuente que V1^V1=V2^V2=0 (vector cero)
y que V1^V2=-V2^V1
Resulta 2 V1^V2
que dividido dos da V1^V2
Es decir el producto vectorial:
(x1;y1;0)^(x2;y2;0)=
(0;0;x1y2-x2y1)
Por eso un área suele representarse con un vector perpendicular a la superficie.
Si en lugar de dos vectores en el plano (2x2) tengo tres vectores en el espacio (3x3)
el determinante es igual al volumen del paralelepípedo.
(o el doble del tetraedro)
TOMADO DE:http://www.todoexpertos.com/categorias/ciencias-e-ingenieria/matematicas/respuestas/1307147/determinantes
TEORÍA O DEFINICIÓN
En matemáticas se define el determinante como una forma multilineal alternada de un cuerpo. Esta definición indica una serie de propiedades matemáticas y generaliza el concepto de determinante haciéndolo aplicable en numerosos campos. Sin embargo, el concepto de determinante o de volumen orientado fue introducido para estudiar el número de soluciones de los sistemas de ecuaciones lineales.
Suscribirse a:
Comentarios (Atom)
